Most of statistics is just trying to logically move through the steps.
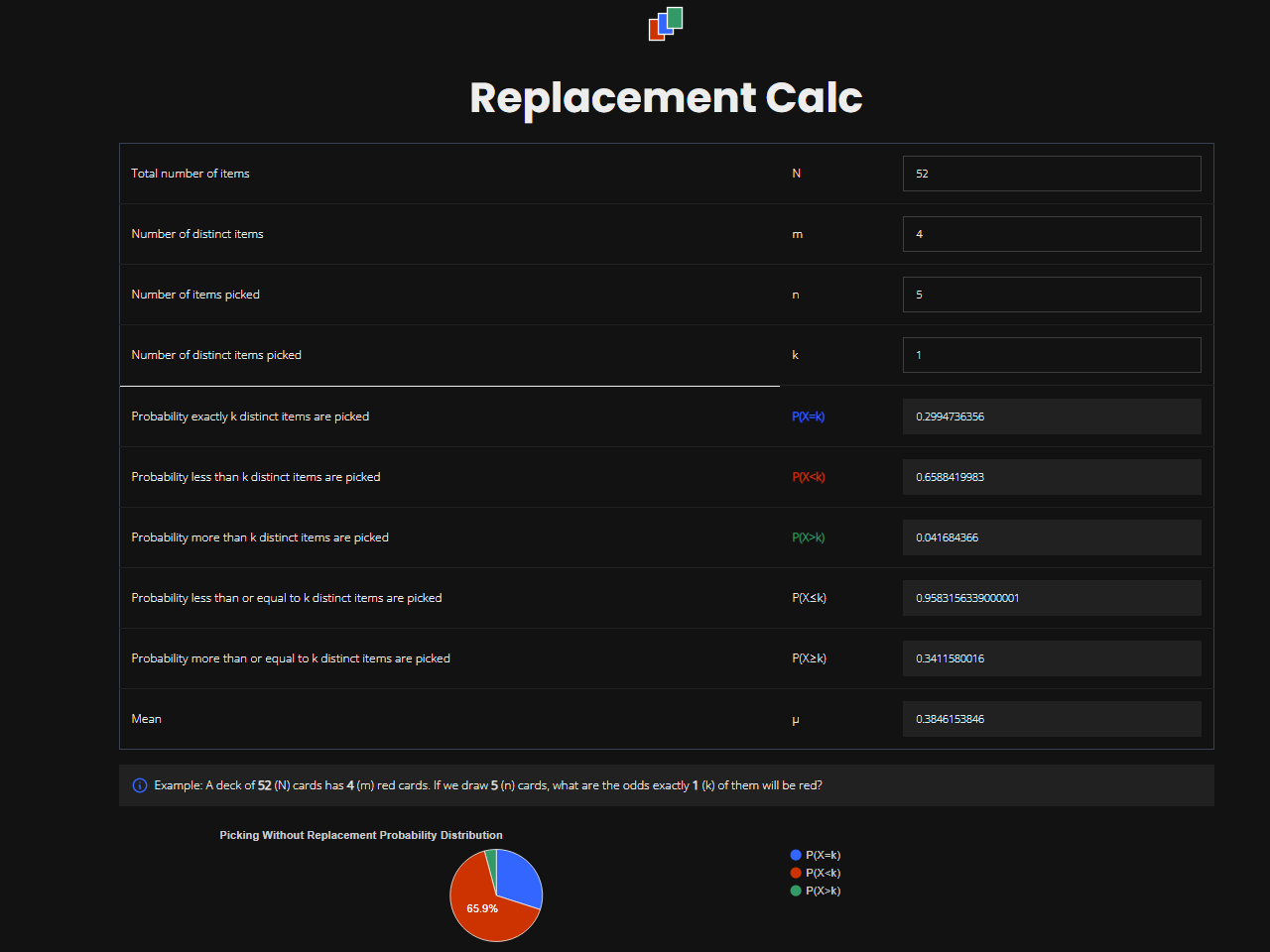
For example, the odds of drawing any given card in a 52 card deck is 1/52. There are 13 hearts so the odds begin as 13/52.
Assuming the first two cards played were hearts, the odds of an individual draw being a heart would be 11/50.
You now compare the number of scenarios where you “win” to the number where you lose. There are two scenarios where you “win” since you said at least 3. The odds of drawing exactly 3 and the odds of drawing exactly 4. You calculate those two odds and add them together. First let’s calculate drawing exactly 3.
*
note; adding all probabilities together should = 1. By that I mean the odds of drawing 0/4, 1/4, 2/4, 3/4, and 4/4 being hearts. At those represent all possible outcomes it reasons that adding all those outcomes together should be 1 (or 100% probability)
There are 11 hearts left, and you need to draw 3. So the number of possible combinations is: 11!/((11-3)! * 3!)
The last card can be anything, so the number of possible combinations out of the remaining cards would be: 39!/((39 - 1)! * 1!)
You multiply those two numbers and divide it by the total number of possible 4 card hands out of the remaining cards: 50!/((50 - 4)! * 4!)
Doing that math gets me 165 * 39/230300 = ~0.0279 = ~2.79%
Repeating that math for drawing 4 hearts gets me: 330/230300 = ~0.00143 = ~0.143%
So that’s approximately ~2.933%
For good measure, I added up the other probabilities and they did indeed = 100%. If you are interested in calculating card draw probabilities permutations is what you are looking for. I included some instructional links.
Hopefully this was helpful. I tried to explain it in such a way that you could replicate it yourself with different numbers. It’s been a bit since I took statistics so it was fun to do some again.
Permutations and combinations have uses in math classes and in daily life. Thankfully, they are easy to calculate once you know how. Unlike permutations, where group order matters, in combinations, the order doesn't matter. Combinations...

www.wikihow.com
I'm currently doing a probability unit, and one of the formulas I have learned is: $$n_{C_{x}} (P^{x}) (1-p)^{n-x}$$ So for example: James is practicing penalties. His chance of scoring with eac...

math.stackexchange.com